

This is a short review on coded aperture imaging. This paper appeared in a longer version in In 't Zand (1992). A postscript version of the complete paper (original version, without figures) is available (220 kB).
The text is regularly updated for new developments in the field.
Last update: March 7, 1996.
An alternative class of imaging techniques employs straight-line ray optics
that offer the opportunity to image at higher photon energies and over larger
FOV's.
These techniques have one common signature: the direction of the incoming rays
is, before detection, encoded; the image of the sky has to be reconstructed by
decoding the observation afterwards. It is apparent that this method of producing
sky images is a two-step procedure, in contrast to the direct or one-step imaging
procedure of focusing techniques. These alternative techniques are referred to as
multiplexing techniques. Another important difference in an astrophysical
application between both types of imaging concepts is that in multiplexing techniques
an imaged point source experiences the noise of all photons detected over the
whole detector while in focusing techniques it are only the photons in a small
part of the detector. Thus, for equal collecting areas the sensitivity of
a focusing instrument is always better than of a multiplex instrument.
Multiplexing techniques can be divided in two classes: those based on
temporal and those on spatial multiplexing (Caroli et al. 1987).
A straightforward example of temporal multiplexing is the scanning collimator:
when the direction of a collimator is moved across a part of the sky which
contains an X-ray point source, the number of counts per second that is detected
as a function of time has a triangular shape. The position of the maximum of the
triangle provides the position of the source along the scanning direction and
the height of the triangle provides the flux of the source. A second scan along
another direction completes the two-dimensional position determination of the
source. More scans may be necessary if the source is extended or when there are
more sources in the FOV of the collimator. The Large Area Counter (LAC) of the
Japanese X-ray satellite Ginga (Makino et al. 1987 and Turner et al. 1989) is a
recent example of an instrument employing a collimator.
A more sophisticated device that is based on time multiplexing was
introduced by Mertz (1968) and further developed by Schnopper et al. (1968): the
rotation modulation collimator (RMC). RMCs are often used as all-sky monitor.
Several RMCs have flown, for instance in Ariel-V (Sanford 1975),
SAS-3 (Mayer 1972) and Hakucho (Kondo et al. 1981) and in several balloon
experiments (see e.g. Theinhardt et al. 1984). The most recent example is the
Granat observatory which carries 4 RMCs (Brandt et al. 1990). In its basic form
an RMC has the disadvantage of being insensitive to short term fluctuations of
X-ray intensity (with respect to the rotation period of the aperture), because the
very same temporal information must be used for reconstructing the position of
sources. However, techniques to circumvent this problem have been proposed
(Lund 1985).
Temporal multiplexing techniques in principle do not need a position-sensitive
detector, contrary to spatial multiplexing techniques. Spatial multiplexing
techniques can be divided in two subclasses: in the first subclass two or more
collimator grids, widely separated, are placed in front of a detector, and in the
second subclass one or more arrays of opaque and transparent elements are placed
there. Instruments of the former class are called 'Fourier transform imagers'
(Makishima et al. 1978 and Palmer & Prince 1987). These instruments record a number
of components of the Fourier transform of the observed sky, and the observed sky
can be reconstructed by an inverse Fourier transform in a way that is common to
the 'CLEAN' algorithm in radio astronomy.
Instruments of the second subclass are called 'coded-mask systems'.
In the remainder of this text, a short review is given on
the imaging concept of coded-mask systems, dealing separately with each important
component of such a system. Requirements to arrive at an optimum
imaging capability of the whole system are discussed.
Basic concept of coded-mask imaging
A coded-mask camera, to be used to image the sky for photon energies between E1 and
E2, basically consists of:
 a coded mask, i.e. a plate with areas that are transparent or opaque to
photons with energies between E1 and E2. The transparent and opaque areas, or
shortly 'mask elements', all have an equal size and are distributed in a
pre-determined pattern, which is placed on a regular grid. The form of a mask
element may be arbitrary.
a coded mask, i.e. a plate with areas that are transparent or opaque to
photons with energies between E1 and E2. The transparent and opaque areas, or
shortly 'mask elements', all have an equal size and are distributed in a
pre-determined pattern, which is placed on a regular grid. The form of a mask
element may be arbitrary.
 a position-sensitive detector, whose spatial resolution is sufficiently
matched to the mask-pattern grid size and which is sensitive to photons with
energies between E1 and E2.
a position-sensitive detector, whose spatial resolution is sufficiently
matched to the mask-pattern grid size and which is sensitive to photons with
energies between E1 and E2.
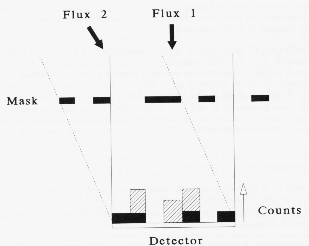
Figure: basic concept of coded-mask imaging. Two point sources illuminate a position-sensitive detector through a mask. The detector thus records two projections of the mask pattern. The shift of each projection encodes the position of the corresponding point source in the sky; the 'strength' of each projection encodes the intensity of the point source
The principle of the camera is straightforward: photons from
a certain direction in the sky project the mask on the detector; this projection
has the same coding as the mask pattern, but is shifted relative to the central
position over a distance uniquely correspondent to the direction of the photons.
The detector accumulates the sum of a number of shifted mask patterns. Each shift
encodes the position and its strength encodes the intensity of the sky at that
position. It is clear that each part of the detector may detect photons incident
from any position within the observed sky. After a certain illumination period,
the accumulated detector image may be decoded to a sky image by determining the
strength of every possible shifted mask pattern.
Proper performance of a coded-mask camera requires that every sky position is
encoded on the detector in a unique way. This can be stated in terms of the
autocorrelation function of the mask pattern: this should consist of a single
peak and flat side-lobes (a delta function). This puts constraints on the type
of mask pattern and on the way its (shifted) projections are detected.
An important difference to direct-imaging systems is the fact that Poisson noise
from any source in the observed sky is, in principle, induced at any other
position in the reconstructed sky.
The imaging quality of the camera is determined by the type of mask pattern, the
optical design of the camera, the spatial response of the detector and the
decoding (or reconstruction) method.
Mask patterns
In view of the imaging performance, one would want the mask pattern to satisfy the
following conditions:
 the autocorrelation function of the mask pattern should be a delta function;
the autocorrelation function of the mask pattern should be a delta function;
 the signal-to-noise ratio of a coded sky source should be optimum.
the signal-to-noise ratio of a coded sky source should be optimum.
Both Fresnel zone and random pinhole mask patterns are not ideal with respect to the first condition, the patterns possess autocorrelation functions whose sidelobes are not perfectly flat. Later work concentrated on finding patterns, based on the idea of the random pinhole pattern, that do have flat side-lobes. Ideal patterns were found that are based on cyclic difference sets (Gunson & Polychronopulos 1976, Fenimore & Cannon 1978).
A cyclic difference set D, characterized by the parameters n, k and z, is
a collection of k integer numbers {I1, I2,...,Ik} with values Ii between 0 and
n such that for any J=/0 (mod n) the congruence Ii-Ij=J
(mod n) has exactly z solution pairs (Ii,Ij) within D (Baumert 1971).
An example of a cyclic difference set D with n=7, k=4 and z=2 is the
collection {0,1,2,4}. Cyclic difference sets can be represented by a binary
sequence a_i (i=0,...,n-1) with a_i=1 if i is a member of D and a_i=0
otherwise. In the above example a_i is given by 1110100. a_i in turn can
stand for the discretized mask pattern, assigning a transparent element to
a_i=1 and an opaque one to a_i=0. The cyclic autocorrelation c_l of a_i
is (Baumert 1971):
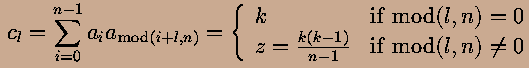
i.e. a single peak on a flat background. A mask pattern based on a_i
consequently satisfies condition 1. a_i has the characteristic that every
difference i-j between a pair of a_i,a_j=1 is equally sampled and therefore
these arrays are also called Uniformly Redundant Arrays
(URA, Fenimore & Cannon 1978).
From the autocorrelation it can be anticipated that it is advantageous with respect to condition 2 to have a difference between k and z that is as large as possible, for k determines the signal and z the background level (and its noise) (note: the argument followed here to meet condition 2 is simplified. In fact, the optimum open fraction of the mask pattern is also dependent on specific conditions concerning the observed sky. See e.g. Skinner 1984 and In 't Zand, Heise & Jager 1994). The maximum difference is reached if n=4t-1, k=2t-1 and z=t-1 if t is integer. These cyclic difference sets are called Hadamard difference sets (Hall 1967 and Baumert 1971) and can be classified in at least three types, according to the value of n:
 Quadratic residue sets: n is prime (the members of this set are given
by the squares, modulo n, of the first (n+1)/2 integers);
Quadratic residue sets: n is prime (the members of this set are given
by the squares, modulo n, of the first (n+1)/2 integers);
 Twin prime sets: n=p(p+2) for integer p, p and p+2 being prime;
Twin prime sets: n=p(p+2) for integer p, p and p+2 being prime;
 Pseudo-noise sets: n=2^m-1 (m>1 is integer).
Pseudo-noise sets: n=2^m-1 (m>1 is integer).
A way to construct a pseudo-noise Hadamard set is the following (Peterson 1961):
if p(0),...,p(m-1) are the factors of an irreducible polynomial of order
m (p(i) is 0 or 1) then a_i is defined by a shift register algorithm:
a_{i+m} = sum over j from 0 to m-1 p(j) a_{i+j} (i = 0,..., 2^m-2-m) (mod 2)
The first m values of this recursive relation, a_0,...,a_{m-1}, can be chosen
arbitrarily: a different choice merely results in a cyclic shift of a_i.
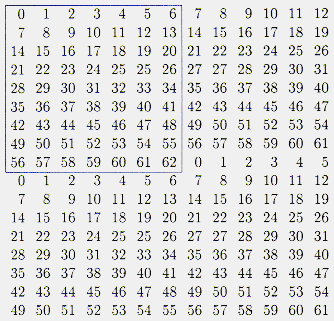
If n can be factorized in a product of two integers (n=p X q), it is possible to construct a two-dimensional array a_{i,j} (i=0,...,p-1; j=0,...,q-1) from the URA a_i (i=0,...n-1). The mask pattern thus arranged is called the 'basic pattern'. The ordering of a_i in two dimensions should be such, that the autocorrelation characteristic is preserved. This means that in a suitable extension of the basic p X q pattern, any p X q section should be orthogonal to any other p X q section. A characteristic of a URA a_i is that any array a_i^s, formed from a_i by applying a cyclic shift to its elements (a_i^s = a_{mod(i+s,n)}), is again a URA which is orthogonal to a_i. Therefore, the autocorrelation characteristic of the expanded a_{i,j} is fulfilled if every p X q section is a cyclic shift of the basic pattern. Two examples of valid ordering methods are shown in the following figure:

The pseudo-noise arrays have the convenient property that they can easily be wrapped in almost a square of n>>1: if m is even, n can be written as n=2^m-1=(2^{m/2}}-1)(2^{m/2+1), so that p and q only differ by 2.
Several practical problems arise in the manufacturing of a two-dimensional mask plate. One in the X-ray regime is that an opaque mask element may be completely surrounded by transparent elements. In the X-ray regime it is necessary to keep transparent elements completely open, because the use of any support material at open mask elements soon results in too much attenuation of flux. Thus, an isolated opaque mask element will not have any support. Two methods may be applied to solve this problem:
 Choose a mask pattern where no isolated opaque elements occur. Such
patterns exist and are called 'self-supporting'.
Choose a mask pattern where no isolated opaque elements occur. Such
patterns exist and are called 'self-supporting'.
 Include a support grid in the mask plate.
Include a support grid in the mask plate.
At photon energies above 10 keV this issue of support is less constraining because at these energies transparant materials can easily be found that support opaque mask elements from above or below instead of from the sides.
Another practical problem of masks occurs in applications beyond a few hundred keVs: the opaque elements generally need to be very thick, in the order of centimeters instead of 100s of microns. This means the mask element sizes cannot be smaller than that because otherwise the mask itself would act as a narrow-field collimator.
The autocorrelation characteristic remains valid only if the coding is performed by the use of a complete cycle of a basic pattern. As soon as the coding is partial, systematic noise will emerge in the side-lobes of the autocorrelation function. This noise can be interpreted as false peaks and thus deteriorates the imaging quality. In order to be able to record for every position in the observed sky a full basic pattern, one needs a special optical configuration of mask and detector (see next section). Sometimes also a mask is needed that consists of more than 1 basic pattern. How such a mosaic mask is constructed has been discussed above.
Recent developments in mask design seem to concentrate on the introduction of
two-scaled mask patterns (Skinner & Grindlay 1992) and masks with
open fractions of less than 50% (In 't Zand, Heise & Jager 1994). A two-scaled
mask has 2 potential advantages: such a mask might increase the passband
where it can be applied and it might enable a two-stepped CPU-efficient search
for transient events (first, searching at a rough resolution to limit the
field-of-view to search in and, second, locate the event accurately).
A low open-fraction mask employs early suggestions to optimize the signal-to-noise
ratio of point sources, and at the same time limit the telemetry rate.
Both two-scaled and low-open-fraction masks bring along one problem which
has not been satisfactorily solved yet: no such patterns have been found
with ideal autocorrelation functions (with a few exceptions at particular
open fractions). In certain applications this is less of a problem, and
validates even the return of the random patterns (In 't Zand et al. 1995).
Optical design
The optical design of a coded-mask camera is defined by the sizes of the mask,
the mask elements and the detector, the number of basic patterns used in the
mask, the distance between mask and detector and the size and place of an
optional collimator. Apart from the imaging quality, the design determines the
angular resolution and the FOV (the latter is usually expressed in the full-width
at half maximum, FWHM, of the collecting area across the observed sky).
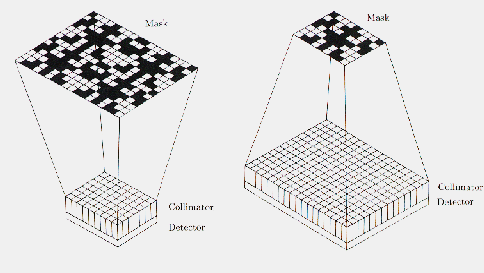
Figure: schematic drawings of the two types of 'optimum' configurations discussed in the text. The left configuration is called 'cyclic'. Note the collimator, placed on top of the detector, necessary to confine the FOV to that part of the sky in which every position will be coded by one full basic pattern. From Hammersley (1986)
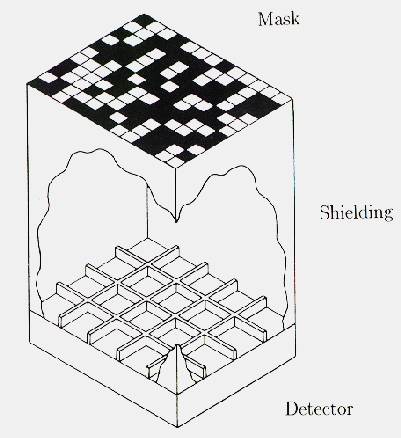
Figure: Schematic drawing of the 'simple' configuration. The sizes of the mask and detector are equal. Note that instead of a collimator, as in the optimum configurations, a shielding is used. The shielding prevents photons not modulated by the mask pattern to reach the detector. From Hammersley et al. (1992)
 The mask consists of one p X q basic pattern, while the detector
has a size of (2p-1) X (2q-1) mask elements.
By the implementation of a collimator in front of the
detector, the observed sky is restricted to those positions in the sky from where
the mask is completely projected on the detector.
The mask consists of one p X q basic pattern, while the detector
has a size of (2p-1) X (2q-1) mask elements.
By the implementation of a collimator in front of the
detector, the observed sky is restricted to those positions in the sky from where
the mask is completely projected on the detector.
 The mask consists of a mosaic of almost 2 X 2 cycles of the
basic pattern ((2p-1) X (2q-1) mask elements), while the detector is as
large as one basic pattern. A collimator is
implemented, to restrict the observed sky, as seen from any position on the
detector, to that part of the sky seen through one complete cycle of the basic
pattern. This type of configuration often is called 'cyclic' because of the
nature of the mask.
The mask consists of a mosaic of almost 2 X 2 cycles of the
basic pattern ((2p-1) X (2q-1) mask elements), while the detector is as
large as one basic pattern. A collimator is
implemented, to restrict the observed sky, as seen from any position on the
detector, to that part of the sky seen through one complete cycle of the basic
pattern. This type of configuration often is called 'cyclic' because of the
nature of the mask.
The above types of mask/detector configurations are called 'optimum systems' (Proctor et al. 1979) in the sense that the imaging property is optimum. An alternative configuration is the 'simple' or 'box-type' system. In this system the need for full coding is relaxed. The detector has the same size as the mask, which consists of one basic pattern. No collimator is then needed on the detector; instead a shielding is used to prevent photons that do not pass the mask from entering the detector. In a simple system only the on-axis position is coded with the full basic pattern, the remainder of the FOV is partially coded. Obviously, the off-axis sources will cause false peaks in the reconstruction. However, as will be discussed later on, this coding noise can be eliminated to a large extent in the data-processing, provided not too many sources are contained in the observed part of the sky.
If one assumes for the moment that coding noise is not relevant, the question arises how the simple system compares to the cyclic system. In order to do this comparison, it seems fair to impose on both systems the same FOV and sensitivity. This means that both have a detector of equal size, but in the cyclic system the 2 X 2 mosaic mask is two times closer to the detector than in the simple system, with an appropriate adjustment of the collimator's dimensions. Therefore, the angular resolution in the cyclic system is two times worse in each dimension than in case of the simple system. Most important in the comparison is the following difference between the cyclic and the simple system, concerning the reconstruction of the flux from an arbitrary direction within the observed sky: in the cyclic system all detected photons on the complete detector may potentially come from that direction, while in the simple system only photons from the section of the detector not obscured by the shielding are relevant. Therefore, Poisson noise will affect the reconstruction in the cyclic system stronger than in the simple system. Thus, regarding the Poisson noise, the simple system is superior in sensitivity to the cyclic system (except for the on-axis position where both systems have equal properties). This conclusion is in agreement with the findings of Sims et al. (1980), who have studied the performance of both systems via computer simulations.
Reconstruction methods
Coded-mask imaging is basically a two-step procedure. After the accumulation of
spatially coded detector data, the second step involves the decoding of this
data, in other words the reconstruction of the observed part of the sky.
Since a powerful computer is needed for the
reconstruction process, this is usually done off-line (particularly if the number
of mask elements is large). Several reconstruction algorithms are in use. The
choice for a certain algorithm depends on the specific aim (e.g. search for
detections of unexpected events or timing analysis of a restricted part of the
sky), the available computer resources and the type of instrument configuration.
Several types of algorithms may in fact be subsequently used on the same set of
detector data. This section gives a short resume of various algorithms. For
clarity the discussion is illustrated with one-dimensional examples and space
is discretized in steps of a size equal to that of a mask element; the
conclusions do not basically differ for two dimensions and smaller steps.
The basic problem to be solved concerns the following. Let the one-dimensional
vector d describe the detector (in units of counts per detector-element
area), s the sky (in counts per mask element area) and b the
detector background (this includes all flux which is not modulated by the mask
pattern, in counts per detector element area). Suppose the detector elements are
as large as a mask element. The detection process can then be described by:
d = C s + b
where C is a matrix whose rows contain cyclic shifts of the basic mask
pattern. An element of C is 1 if it corresponds
to an open mask element and 0 otherwise. In the case of an optimum system with a
basic mask pattern of n elements, d, s and b contain
n elements and C n X n elements. In the case of a simple system
with a mask of n elements, d and b contain n elements, the
sky vector s contains 2n-1 elements and the matrix C contains
(2n-1) X n elements. The problem to be solved is
to reconstruct s out of this set of linear equations. Although b
is unknown also, one is in principle not interested in it. An approximation for
b is: b is homogeneous over the detector plane, i.e.
b = b i
where i is the unity vector (consisting of only ones), b is now a
single unknown scalar.
M=(1+P) C^T-P U
where C^T is the transposed of C and U is the unity matrix
(consisting of only 1's and having the same dimensions as C^T). P is
a constant and is determined from an analysis of the predicted cross correlation
value: a prediction of the reconstruction can be easily evaluated if one assumes
that the mask pattern is based on a cyclic difference set and the camera
configuration is optimum. The expected value of the cross correlation is then
(using the autocorrelation value for cyclic difference sets):
Md = M (Cs + bi) = (1+P )(k-z) s + [ { (1+P )z - P k} sum s_i + { (1+P )k - P n} b ]i
Apart from a scaled value of s, which is the desired answer, the result
also includes a bias term (the i-term). It is not possible to eliminate
this bias by a single value of P. Rather, the sum s_i factor or the b
factor can be canceled separately. Canceling the sum s_i factor involves a
value P of
P_1 = z/(k-z) = (k-1)/(n-k),
canceling the b-factor involves P to be (note: An interesting
characteristic of the reconstructed sky is the sum of the reconstructed values.
In case P =P_1 this is sum Md = k sum s_i + nb, i.e.
the sum of all detected counts. If P =P_2 this sum is equal to 0.):
P_2 = k/(n-k)
Since k/n is the open fraction, t, of the mask pattern, P_2 can be written as:
P_2 = t/(1-t).
P_1 approximates P_2 if k>>1. The reconstruction value then reduces to:
Md = ks.
Normalizing M results in:
M/k=n/k(n-k)X(C^T-k/nXU.
In the case of a simple system, this would also apply if the 'hard' zeros in C (i.e. zeros that do not arise from zero a_i-values, were replaced by cyclically shifted a_i's. The result would then imply: (Md)_i=(Md)_(mod(i+n,2n-1)); this is a consequence of the fact that 2n-1 unknowns are to be determined from a set of only n linear equations, which is under-determined in general. In this formulation a source at position i causes a false peak of the same strength at position mod(i+n,2n-1). If the 'hard' zeros in C are not replaced, this does not apply directly, but an interdependence in the solution for the reconstruction remains. This interdependence is not so strong: one real peak will cause many small ghost peaks rather than a single false peak which is just as strong as the real peak. It is then possible to find a unique solution for s as long as it does not have more non-zero values than n. This search is accomplished by testing reconstructed peaks on their authenticity, the reconstruction process is then necessarily iterative.
W(omega) = C(omega) / ( |C(omega)|^2 + S/N(omega)^{-1} )
Because S/N is not known before the reconstruction is completed, a frequency-independent expression is used for it.
It is clear that Wiener filtering is especially helpful if the mask pattern is not ideal, which is the case for random and Fresnel zone patterns. However, ideal patterns such as those based on cyclic difference sets are characterized by flat modulation transfer functions (all spatial frequencies are equally present for URA-patterns, which is apparent from the definition of URAs. Sims et al. (1980) confirmed this via computer simulations and found this also to be the case if an ideal pattern is used in partial coding, such as in a simple system.
One iterative method is the maximum entropy method (MEM). MEM has gained widespread favor in different areas as a tool to restore degraded data. Introductions to the theory behind MEM as applied to image restoration can be found in Frieden (1972) and Daniell (1984), while a review is given by Narayan & Nityananda (1986). Examples of applications of MEM are given by Gull and Daniell (1978), Bryan and Skilling (1980) and Willingale (1981), while the application specifically to images from coded-mask systems are described by Sims et al. (1980) and Willingale et al. (1984). MEM was introduced in the field of coded-mask imaging by Willingale (1979). Despite the good results that can be obtained with this method, a major drawback is the large amount of computer effort required, as compared to linear methods such as cross correlation.
Another iterative method is iterative removal of sources (IROS). IROS is in fact an extension of the cross correlation method and was introduced by Hammersley (1986) as a procedure to eliminate problems due to incomplete coding (also called 'missing data') in simple systems. The advantage of IROS is that it is much more CPU efficient than MEM. The principle of IROS is as follows: 1) do a cross correlation; 2) find the strongest point source; 3) subtract the expected detector exposure by this point source from the observed detector; 4) goto 1 or, if there is no point source left, put point sources back into last cross correlation image. This procedure will ensure that any coding noise due to point sources is suppressed to a level below the statistical noise and thus ensures an unbiased determination of point source intensities and positions. One can enhance the CPU efficiency by dealing with more than 1 point source in each iteration (in a smart way which is not discussed here).



 Go back to Coded Aperture Imaging main page
Go back to Coded Aperture Imaging main page
March 7, 1996